Transformer Architecture

This is a page to store resources and thoughts about transformer architecture and its applications.

Components of the Transformer Architecture

Tokenization

The tokenization step takes the raw input and partitions it into tokens, bit-sized chunks of the data. Tokens are the unit of analysis of the transformer model, and the universe of all possible tokens is called the models “vocabulary.” For the sentence, “I am Kong”, example output of a tokenizer is the list [“I”, ” am”, ” Kong”]. Each of the tokens in the vocabulary have an assigned unique ID. Common embedding models now have a vocabulary of 30,000-50,000 tokens.

Embedding

The embedding step takes the input token IDs and converts them to vectors in a topic or “meaning” vector space. Outside of training, this just behaves like a lookup tool — token ID in, embedding vector out. This is a dimensional reduction from the full vocabulary and these vectors are typically on the order of 300-3000 dimensions. For example, the input sentence “I am Kong” might be represented as three 768-dimensional vectors.

Positional Encoding

Transformers need to know the relative position of each input token in order to understand the relationship between the tokens (or at least this makes them much better at predicting the next token in the sequence). The relative position of each token is transformed and added to the input token vectors. This sounds like a simplification, but really, the relative position is encoded into each token vector by adding small numbers to each element of the token vector. The gist is that you need to add a unique position vector of the same dimension to each token vector before putting it into the transformer model.

The formulas for these positional encodings were hard for me to understand — this is a video I found very helpful:

If you get into the details of positional encoding, you’ll likely encounter these equations from the original Attention Is All You Need paper that give you what numbers you should add to each element of the token vector:

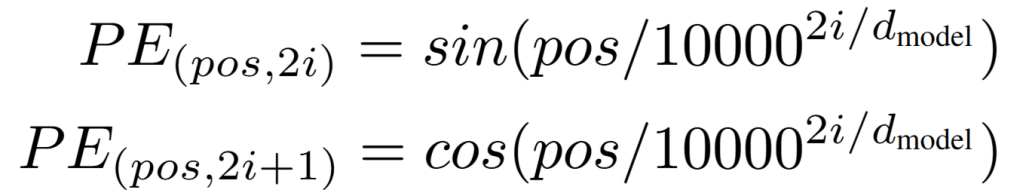
It took me a while to understand what the variables are in these equations, and I haven’t yet found a great resource that explains it the way I want (this one comes close). So I will give you my interpretation.

• pos is the position of the token in the input sequence. For the token sequence [“I”, ” am”, ” Kong”], the “I” token has position 0 and ” Kong” has the position 2.
• d is the dimensionality of the embedding vector (d=768 in the example from earlier).
• i is the element of the vector that you will be adding the number to — almost. Note that there are two functions above. The sine function represents the even elements, and cosine represents the odd elements. i represents the ith even or ith odd element, so we actually need to divide the element by 2. For example, if you were calculating the PE for the 0th element, it would be i=0 and you use the sine function. For the 5th element, i=2 and use the cosine function. This is kind of confusing (and annoying) to me.
• The 10,000 just needs to be a large enough number compared to the context window of the model that the sine and cosine do not repeat.

I would rewrite this function as

where k is the element index of the d-dimensional embedding vector (so k is between 0 and d-1). pos and i are the same as before. I think this is more interpretable, however the previous formula is easier to program since you just iterate i 0 through d/2 and update all the elements based on 2i and 2i+1.

Transformer

The 3Blue1Brown video on transformers (and the two videos after that explaining the attention and feed-forward layers) are great for understanding how a transformer model works, and how it is different from the neural networks that came before it.

Prediction layer, SoftMax & Sampling, Autoregressive Loop

I’ll come back and update these if I find any useful or important content.